CLACES DE CONJUNTOS

 clases de conjuntos 

Existen varios tipos de conjuntos que se destacan por sus características especiales.  Conocerlos te ayudará a comprender mejor la estructura y el mundo de los conjuntos. 

                                     INTRODUCCION

El estudio de los conjuntos es uno de los conceptos fundamentales en las matemáticas, ya que permite organizar y clasificar objetos de manera lógica. Un conjunto es una colección bien definida de elementos, que pueden ser números, letras, personas, objetos, entre otros. A través de esta clase, los estudiantes aprenderán a identificar y representar conjuntos, reconocer sus elementos, utilizar símbolos matemáticos relacionados y realizar operaciones básicas como la unión, intersección y diferencia. Comprender los conjuntos es esencial, ya que sirven como base para muchos otros temas matemáticos más avanzados y tienen aplicaciones en la vida diaria, en áreas como la informática, la lógica y la estadística.

Conjunto universal 

Con el ánimo de evitar confusiones, cuando definimos un conjunto debemos especificar de dónde se están tomando los elementos que lo conforman.  Esto significa que debe existir una base de la cual tomamos estos elementos, esta base sobre el cual trabajamos es llamada conjunto universal.  Usaremos siempre la letra  para representar el conjunto universal.

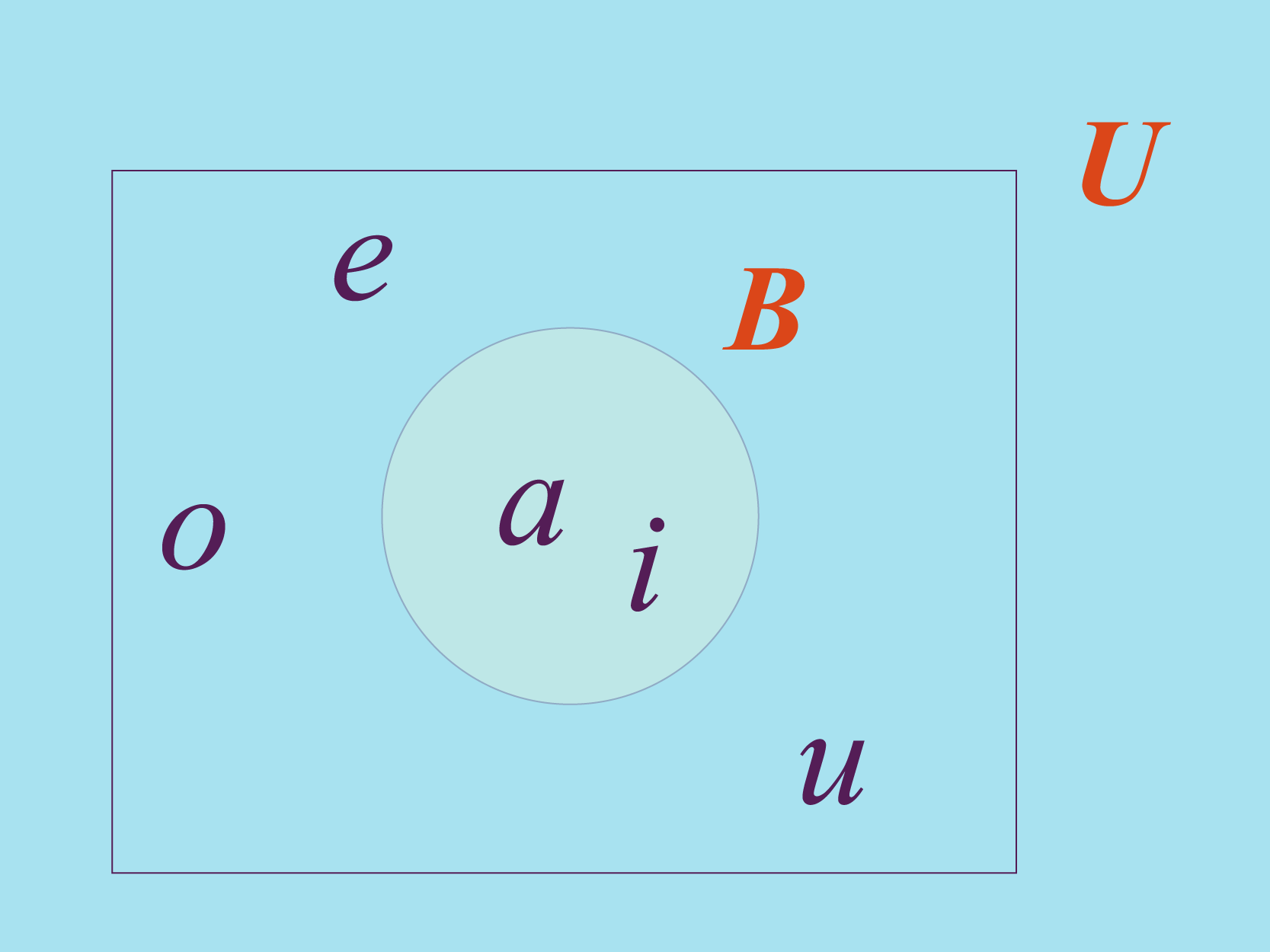
Por ejemplo, si quieres definir  como el conjunto conformado por las vocales  e , el conjunto universal podría ser el conjunto de las vocales.  En la figura anterior se muestra cómo puedes usar los diagramas de Venn para representar la relación entre el conjunto  y su conjunto universal .

Observa que el conjunto universal puede tener exactamente los elementos de los conjuntos que abarca o más.

Conjunto vacío

Consideremos la existencia de un conjunto que no tiene elementos, este es llamado conjunto vacío.  Para representar dicho conjunto usamos el reconocido símbolo del vacío, como se muestra en la imagen de abajo:

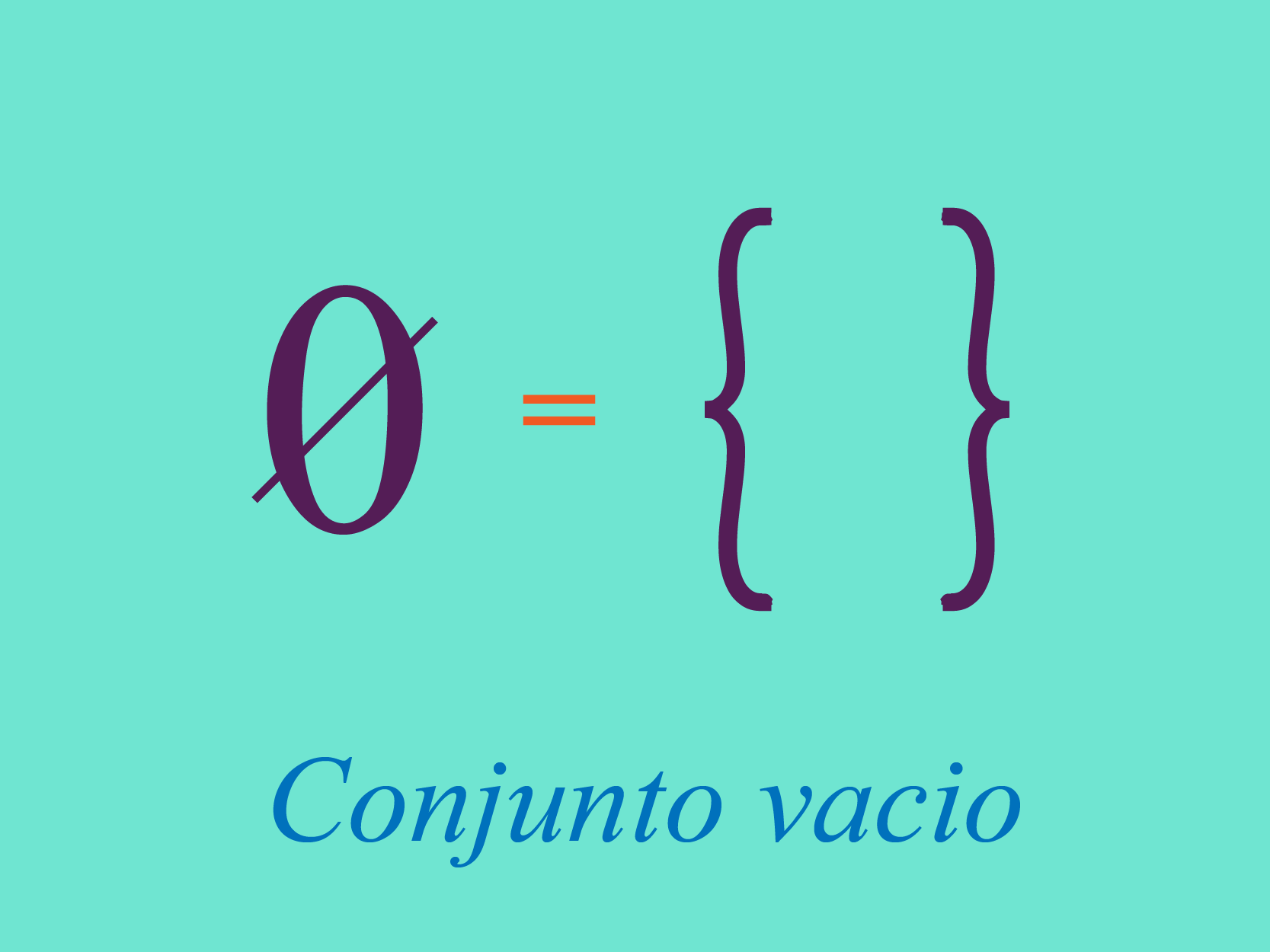
También, haciendo uso de la descripción por extensión, representamos el conjunto vacío por medio de los corchetes .  Como el conjunto vacío no tiene elementos, no podemos ubicar ningún elemento en el interior de los corchetes.
Conjuntos unitarios

 

El conjunto unitario se distingue por tener solo un elemento.  No importa qué tipo de elemento tenga el conjunto, un gato, un perro, un número, una letra o cualquier otra cosa, si tiene un solo elemento es llamado conjunto unitario.

                                      

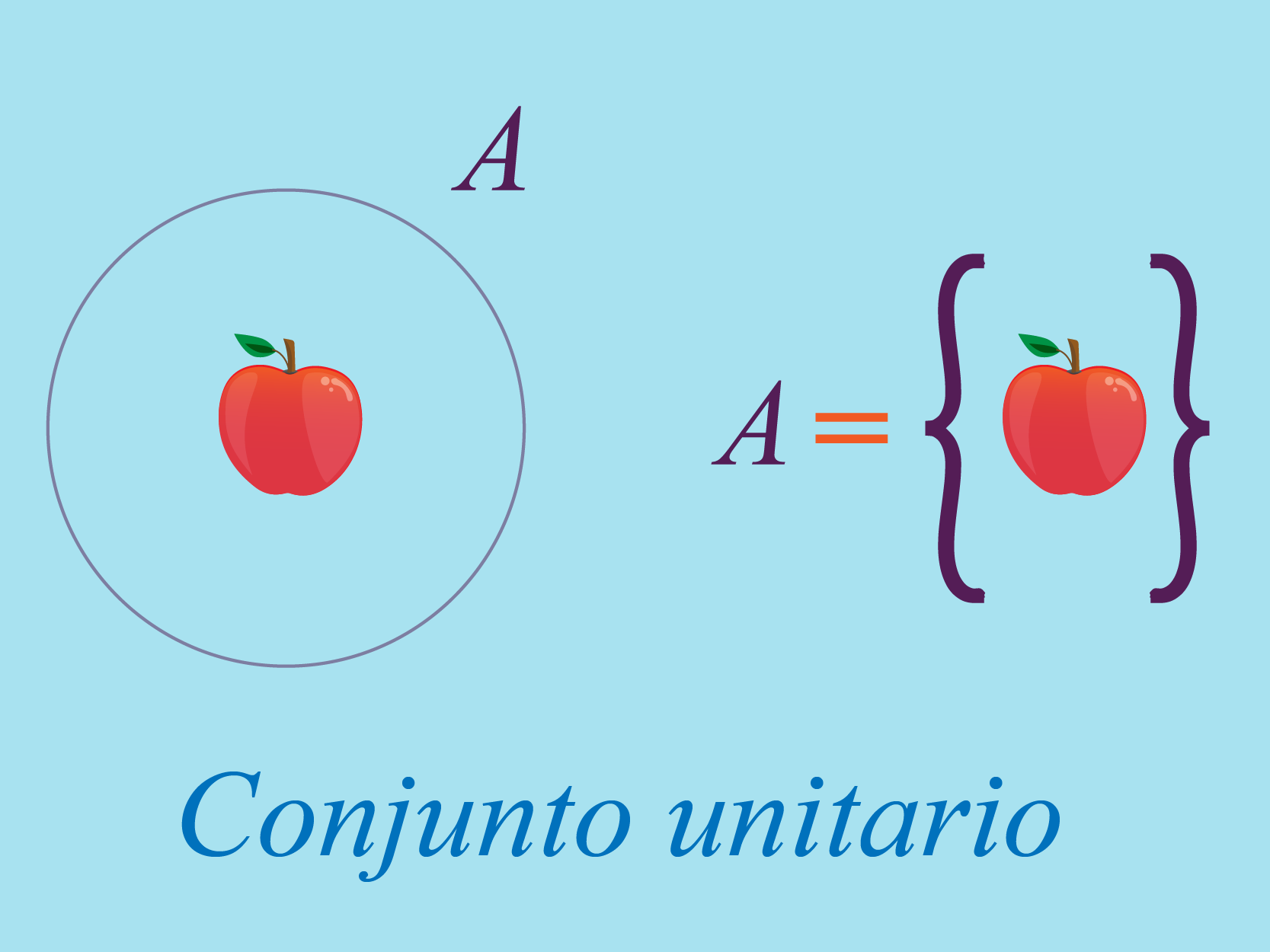
                 conjunto unitario

Conjuntos finitos

Este tipo de conjunto también se distingue por la cantidad de elementos que posee.  Un conjunto es finito si podemos contar la cantidad de elementos que lo conforman.

Por ejemplo, el conjunto de las letras del idioma castellano es finito porque en total son  letras.  En la imagen de la derecha se muestran otros conjuntos finitos.  Te puedes dar cuenta que los conjuntos unitarios también son finitos.

Conjuntos infinitos

No es fácil encontrar en la naturaleza ejemplos de este tipo de conjuntos.  Los conjuntos infinitos son aquellos a los cuales no les podemos contar la cantidad de elementos que los componen.  El método más fácil para representar este tipo de conjuntos es por comprensión.  Basta con mencionar las características que tienen en común los elementos del conjunto y los estaremos determinando a todos.  Considera el conjunto de los números que terminan en tres, podríamos definirlo así:  Sea 

También existe una manera de representar algunos conjuntos infinitos por extensión.  Basta exhibir los primeros elementos del conjunto e indicar con puntos suspensivos que la lista continua indefinidamente.  En el caso del conjunto , definido en el párrafo anterior y conformado por los números que terminan en tres, se tiene 

.

Los ejemplos más sencillos y comunes de conjuntos infinitos los encontramos en los números.  ¿Cuántos números pares hay? ¿cuántos múltiplos tiene el tres?  Estos conjuntos son infinitos, y no es porque este más allá de nuestra capacidad contar la cantidad de elementos que tienen.  Es que es imposible hacerlo porque no hay un número que represente la cantidad de elementos que el conjunto contiene.

No debes confundir los conjuntos infinitos con conjuntos finitos que tienen una gran cantidad de elementos.  Por ejemplo, ¿consideras el conjunto de todos los granos de arena en el planeta Tierra, un conjunto infinito?  En este caso, aunque el conjunto tenga una gran cantidad de elementos debe existir un número que la represente, así sea muy 

Referencias bibliográficas

Baldor, A. (2007). Álgebra. Grupo Editorial Patria.

• Clásico libro de matemáticas que aborda el tema de conjuntos en sus primeros capítulos, con explicaciones y ejercicios.

Larson, R., & Hostetler, R. (2006). Precálculo: Matemáticas para el cálculo. McGraw-Hill.

• Incluye fundamentos sobre conjuntos, operaciones entre conjuntos y diagramas de Venn.

Sánchez, A. (2013). Matemáticas 1. Educación Media Superior. Editorial Trillas.

• Texto utilizado en secundaria y bachillerato, con ejemplos aplicados y teoría clara sobre conjuntos.

Ministerio de Educación de Guatemala (MINEDUC). (2021). Currículo Nacional Base – Nivel Medio.

• Documento oficial que establece los contenidos y competencias relacionadas con conjuntos en el área de matemática.

• Disponible en: https://www.mineduc.gob.gt