Historia de la matemática

La palabra matemáticas proviene del vocablo griego antiguo mathëmatiká, que traduciría algo así como “cosas que se aprenden”.
Esto se debe a que los antiguos distinguían el “arte matemática” (mathëmatiké tékhnë), de otros campos del saber, como el “arte de la música” (mousikë tékhnë), porque la música podía apreciarse a pesar de no haber sido instruido, mientras que la matemática no; para apreciarla hacía falta instruirse en ella.
Sin embargo, lo que comprendemos como matemática, es mucho más antiguo en la historia humana, ya que podría haber tenido el mismo origen temporal que la escritura.
De hecho, se piensa que los primeros intentos por tomar notas escritas correspondían a números y contabilidades, antes que a palabras y sentidos.
Este tipo de sistemas existía ya en el antiguo Egipto y en la antigua Mesopotamia, aunque fueron los griegos los primeros en considerarla una rama de la filosofía.
Los primeros matemáticos griegos datan del siglo VI a. C. y eran los llamados pitagóricos, discípulos de Pitágoras (c. 569 - c. 475 a. C.).
Posteriormente el estudio matemático llamaría la atención del gran filósofo griego Aristóteles (siglo IV a. C.), y más adelante aún del latino Cicerón (106 - 43 a. C.).
Durante el Medioevo fue un campo ampliamente investigado por los alquimistas y estudiosos islámicos, hasta su reaparición en el Renacimiento, al servicio de los saberes humanísticos y científicos renovados en Occidente.
¿Para qué sirve la matemática?

La matemática es una herramienta mental muy poderosa.
Le permite al ser humano realizar una serie vasta y compleja de operaciones que tienen incidencia directa en la vida real, como son la descripción y el análisis de los espacios, las cantidades, las relaciones, las formas, las proporciones y la certidumbre.
Sin ella no sería posible calcular, medir, ni deducir lógicamente, cosas que a diario en nuestras vidas empleamos sin siquiera detenernos a pensar que estamos aplicando los fundamentos de una ciencia sumamente antigua.
Ramas de la matemática
Es posible reconocer unas 5000 ramas de las matemáticas, que tradicionalmente se agrupan en cuatro grandes campos matemáticos “puros”:
- Cantidad. Donde se hallan los números: números naturales, enteros, reales, racionales, complejos, etc.
- Estructura. Donde se emplean los números y sus relaciones para describir y representar formas y conjuntos: álgebra, teoría de números, combinatoria, teoría de grafos, teoría de grupos, etc.
- Espacio. Donde los números están al servicio de la medición del espacio y el cálculo de las diversas relaciones posibles entre representaciones espaciales: la geometría, la trigonometría, la geometría diferencial, la topología, etc.
- Cambio. Donde los números sirven para expresar relaciones cambiantes, movimientos, desplazamientos y el cambio en general: cálculo, cálculo vectorial, sistemas dinámicos, ecuaciones diferenciales, teoría del caos, etc.
Aplicaciones de la matemática
Además de los campos “puros” de la matemática o enteramente formales, existen áreas en que la matemática se dedica al estudio de aspectos de otras áreas del saber, especialmente a la construcción de herramientas para el análisis y la resolución de problemas.
Algunas de ellas son:
- Estadísticas. La matemática aplicada a la probabilidad y a la capacidad de predecir eventos en una escala porcentual o proporcional, para así tomar decisiones informadas.
- Modelos matemáticos. Se emplean las representaciones numéricas como una forma de simulación de aspectos de la realidad, para intentar predecir o comprender en abstracto las relaciones que hay en ella. Es particularmente útil en la informática.
- Matemáticas financieras. Aplicadas al mundo de las finanzas, las matemáticas prestan su lenguaje formal a la expresión de las relaciones económicas y comerciales que componen este aspecto de la sociedad.
- Química matemática. La química la utiliza para expresar las relaciones de proporción que se dan en las diversas y posibles reacciones de la materia.
¿Por qué es importante la matemática?
La matemática permite la expresión por escrito de numerosas relaciones del mundo real, y abre la puerta a cálculos y formulaciones abstractas mucho más complejas.
En el desarrollo humano, esto supuso un crecimiento importante en su capacidad de abstracción y para manejar ideas complejas.
Es un campo de investigación que pareciera árido y desapegado de la vida real, pero del cual se han desprendido gigantescos avances en otras ciencias, industrias y tecnologías, pues de otro modo carecerían de un lenguaje formal para expresar sus operaciones.
Tipos de operaciones

Según Chevallard, Bosch y Gascón, existen tres tipos de operaciones que pueden llevarse a cabo con las matemáticas:
- Emplear matemáticas conocidas. Tomar procedimientos inventados por otros y aplicarlos a problemas propios para resolverlos, empleando como herramientas el saber numérico y lógico acumulado.
- Aprender y enseñar matemática. Ante un problema complejo, podemos recurrir a expertos en la matemática o libros sobre ella, para aprender a emplear métodos desconocidos hasta ahora y expandir nuestra reserva de herramientas numéricas.
- Crear matemáticas nuevas. En caso de que no exista una herramienta matemática que nos sirva para resolver un problema puntual, podemos crear una, tomando como punto de partida las que ya conocemos.
¿Qué ciencias emplean la matemática?
Prácticamente todas las ciencias exactas y sociales, se sirven de la matemática para expresar sus relaciones y contenidos.
Desde la ingeniería, biología, química, física, astronomía y computación, en las que este lenguaje formal es base indispensable, hasta la sociología, arquitectura, geografía, psicología o diseño gráfico, en las cuales juega un rol puntal y determinado.
Inteligencia lógico-matemática

Según el modelo de inteligencias de Howard Gardner en su Teoría de las inteligencias múltiples, la capacidad de emplear la matemática con facilidad y/o rapidez, suele involucrar un aspecto de la mente humana conocido como inteligencia lógico-matemática o lógico-formal.
Se supone indispensable en las personas con vocación científica, y es un tipo de inteligencia que facilita el trabajo con conceptos abstractos o argumentaciones complejas.
Matemáticos famosos
Entre los matemáticos más importantes de la historia se encuentran:
- Pitágoras de Samos (570-495 a. C.)
- Euclides (c. 325 – c. 265 a. C.)
- Leonardo Pisano Bigollo (1170-1250)
- René Descartes (1596-1650)
- Leonhard Euler (1707-1783)
- Andrew Wiles (1953-)
Fuente: https://humanidades.com/matematica/#ixzz89TEYLgVI
Existen varios tipos de conjuntos que se destacan por sus características especiales. Conocerlos te ayudará a comprender mejor la estructura y el mundo de los conjuntos.
Conjunto Universal
Con el ánimo de evitar confusiones, cuando definimos un conjunto debemos especificar de dónde se están tomando los elementos que lo conforman. Esto significa que debe existir una base de la cual tomamos estos elementos, esta base sobre el cual trabajamos es llamada conjunto universal. Usaremos siempre la letra para representar el conjunto universal.
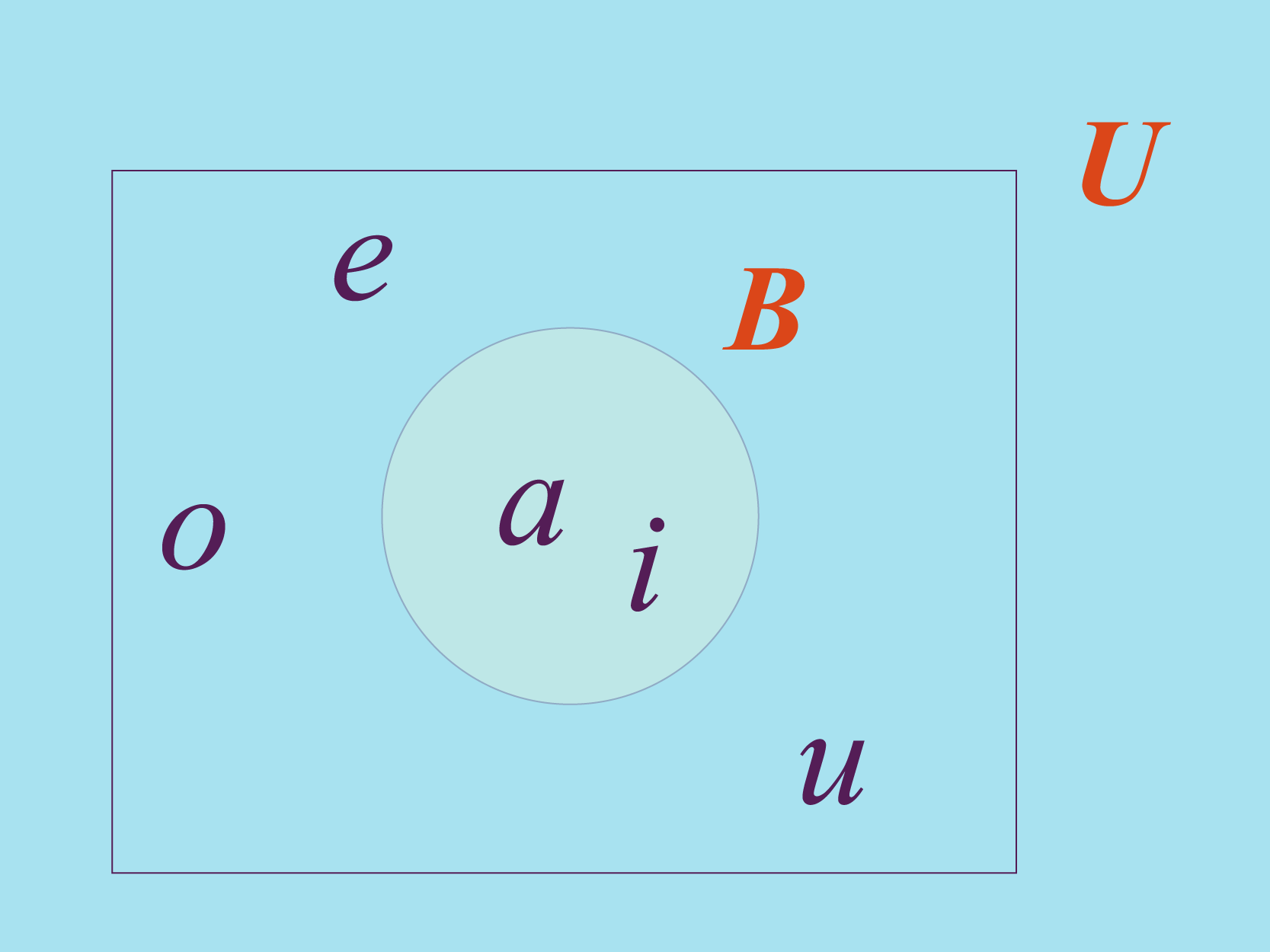
Por ejemplo, si quieres definir como el conjunto conformado por las vocales e , el conjunto universal podría ser el conjunto de las vocales. En la figura anterior se muestra cómo puedes usar los diagramas de Venn para representar la relación entre el conjunto y su conjunto universal .
Observa que el conjunto universal puede tener exactamente los elementos de los conjuntos que abarca o más.
Conjunto vacío
Consideremos la existencia de un conjunto que no tiene elementos, este es llamado conjunto vacío. Para representar dicho conjunto usamos el reconocido símbolo del vacío, como se muestra en la imagen de abajo:
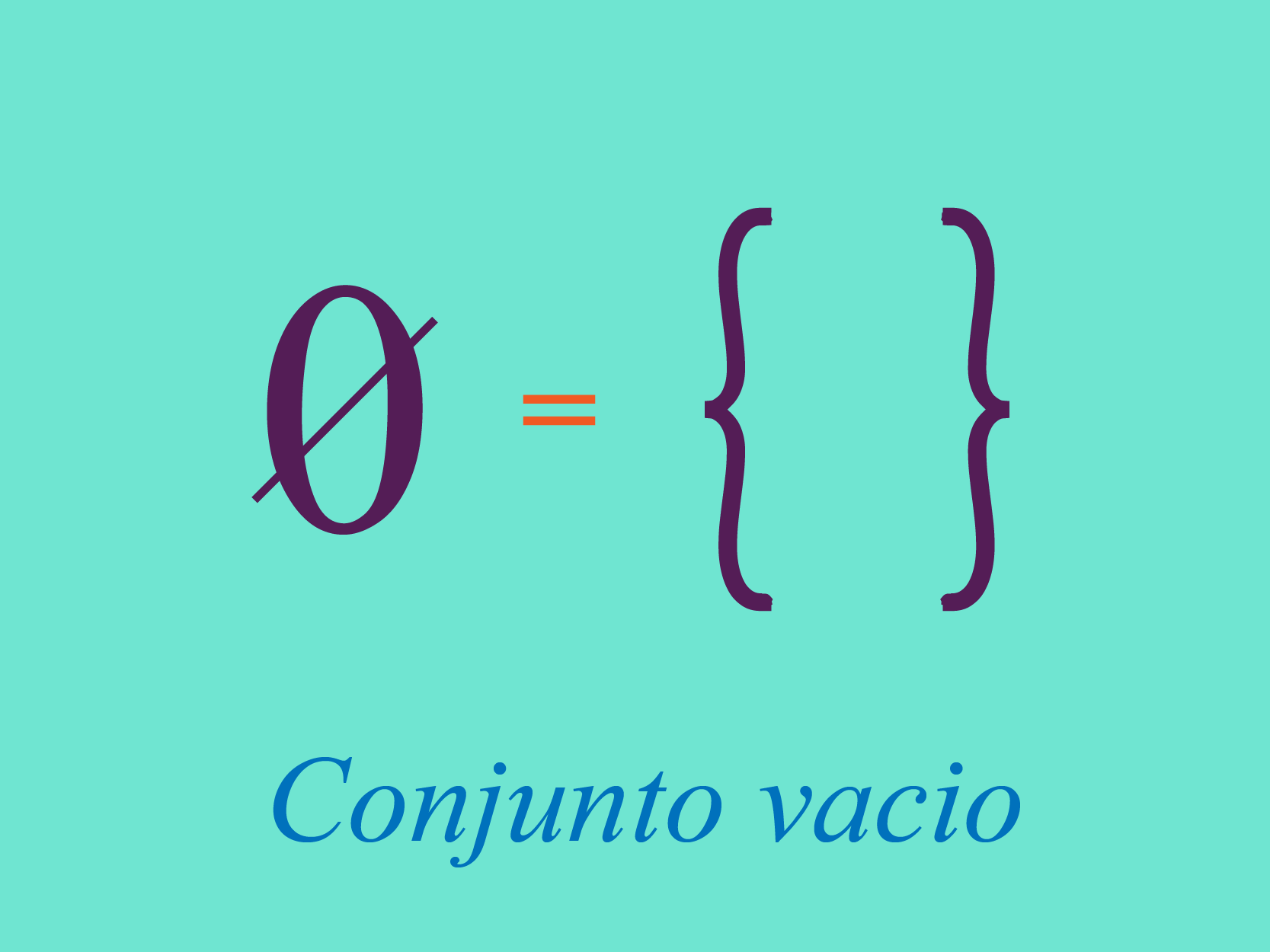
También, haciendo uso de la descripción por extensión, representamos el conjunto vacío por medio de los corchetes . Como el conjunto vacío no tiene elementos, no podemos ubicar ningún elemento en el interior de los corchetes.
Conjuntos unitarios
El conjunto unitario se distingue por tener solo un elemento. No importa qué tipo de elemento tenga el conjunto, un gato, un perro, un número, una letra o cualquier otra cosa, si tiene un solo elemento es llamado conjunto unitario.
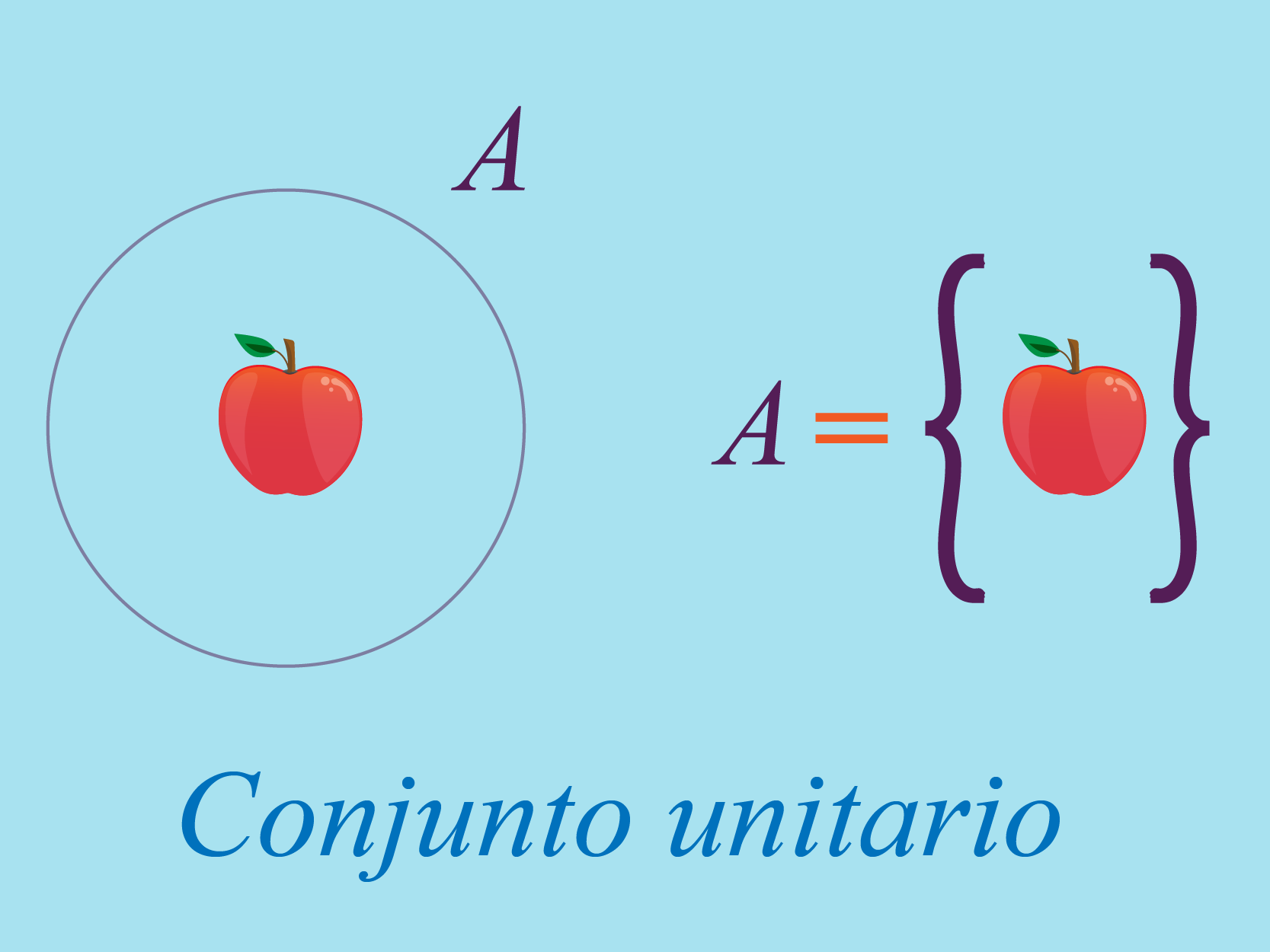
Conjuntos finitos
Este tipo de conjunto también se distingue por la cantidad de elementos que posee. Un conjunto es finito si podemos contar la cantidad de elementos que lo conforman.
Por ejemplo, el conjunto de las letras del idioma castellano es finito porque en total son letras. En la imagen de la derecha se muestran otros conjuntos finitos. Te puedes dar cuenta que los conjuntos unitarios también son finitos.

Conjuntos infinitos
No es fácil encontrar en la naturaleza ejemplos de este tipo de conjuntos. Los conjuntos infinitos son aquellos a los cuales no les podemos contar la cantidad de elementos que los componen. El método más fácil para representar este tipo de conjuntos es por comprensión. Basta con mencionar las características que tienen en común los elementos del conjunto y los estaremos determinando a todos. Considera el conjunto de los números que terminan en tres, podríamos definirlo así: Sea
.
También existe una manera de representar algunos conjuntos infinitos por extensión. Basta exhibir los primeros elementos del conjunto e indicar con puntos suspensivos que la lista continua indefinidamente. En el caso del conjunto , definido en el párrafo anterior y conformado por los números que terminan en tres, se tiene
.
Los ejemplos más sencillos y comunes de conjuntos infinitos los encontramos en los números. ¿Cuántos números pares hay? ¿cuántos múltiplos tiene el tres? Estos conjuntos son infinitos, y no es porque este más allá de nuestra capacidad contar la cantidad de elementos que tienen. Es que es imposible hacerlo porque no hay un número que represente la cantidad de elementos que el conjunto contiene.

No debes confundir los conjuntos infinitos con conjuntos finitos que tienen una gran cantidad de elementos. Por ejemplo, ¿consideras el conjunto de todos los granos de arena en el planeta Tierra, un conjunto infinito? En este caso, aunque el conjunto tenga una gran cantidad de elementos debe existir un número que la represente, así sea muy grande.
Aprende la teoría de conjuntos con símbolos y definiciones fundamentales de forma fácil
La teoría de conjuntos es un área fundamental de las matemáticas que se encarga de estudiar los conjuntos y sus propiedades. Es una rama importante para la comprensión de otros conceptos matemáticos como la geometría, el álgebra y la estadística.
En esta guía, te enseñaremos la teoría de conjuntos con símbolos y definiciones fundamentales de forma fácil y accesible. Con la ayuda de nuestros expertos, podrás aprender los conceptos básicos de la teoría de conjuntos y cómo aplicarlos en la práctica.
Para empezar, definiremos qué es un conjunto. Un conjunto es una colección de objetos, que pueden ser números, letras, o cualquier otro tipo de objeto. Los elementos de un conjunto se representan entre llaves {} y se separan por comas. Por ejemplo, el conjunto de los números enteros positivos menores que 5 se puede representar como {1,2,3,4}.
Además, es importante saber cómo se representan los conjuntos. Los símbolos más comunes son U (unión), ∩ (intersección), ⊆ (subconjunto) y ⊂ (subconjunto estricto). La unión de dos conjuntos A y B se representa como A U B y se refiere a todos los elementos que se encuentran en A o en B. La intersección de A y B se representa como A ∩ B y se refiere a los elementos que se encuentran en ambos conjuntos. El subconjunto de A es un conjunto que contiene todos los elementos de A y se representa como A ⊆ B. El subconjunto estricto de A se representa como A ⊂ B y se refiere a un conjunto que contiene todos los elementos de A pero no todos los de B.
Además, la teoría de conjuntos también incluye otros conceptos importantes, como la diferencia de conjuntos, el complemento de un conjunto y el conjunto vacío. La diferencia de dos conjuntos A y B se representa como A – B y se refiere a los elementos que están en A pero no en B. El complemento de un conjunto A se representa como A’ y se refiere a todos los elementos que no están en A. El conjunto vacío se representa como ∅ y se refiere a un conjunto que no tiene ningún elemento.
La teoría de conjuntos es un área fundamental de las matemáticas, y con esta guía podrás aprender los conceptos básicos de forma fácil y accesible. Aprenderás a representar conjuntos, los símbolos más comunes, y otros conceptos importantes como la diferencia de conjuntos, el complemento de un conjunto y el conjunto vacío. ¡Empieza a estudiar hoy mismo para mejorar tus habilidades matemáticas!
Operaciones entre conjuntos
Además de relacionar los conjuntos a través de la contenencia y la igualdad, podemos crear unos nuevos a través de las operaciones entre conjuntos. Aquí aprenderás de que se trata.
Unión de conjuntos
Supongamos que tenemos los conjuntos y definidos como se muestra en la siguiente figura:
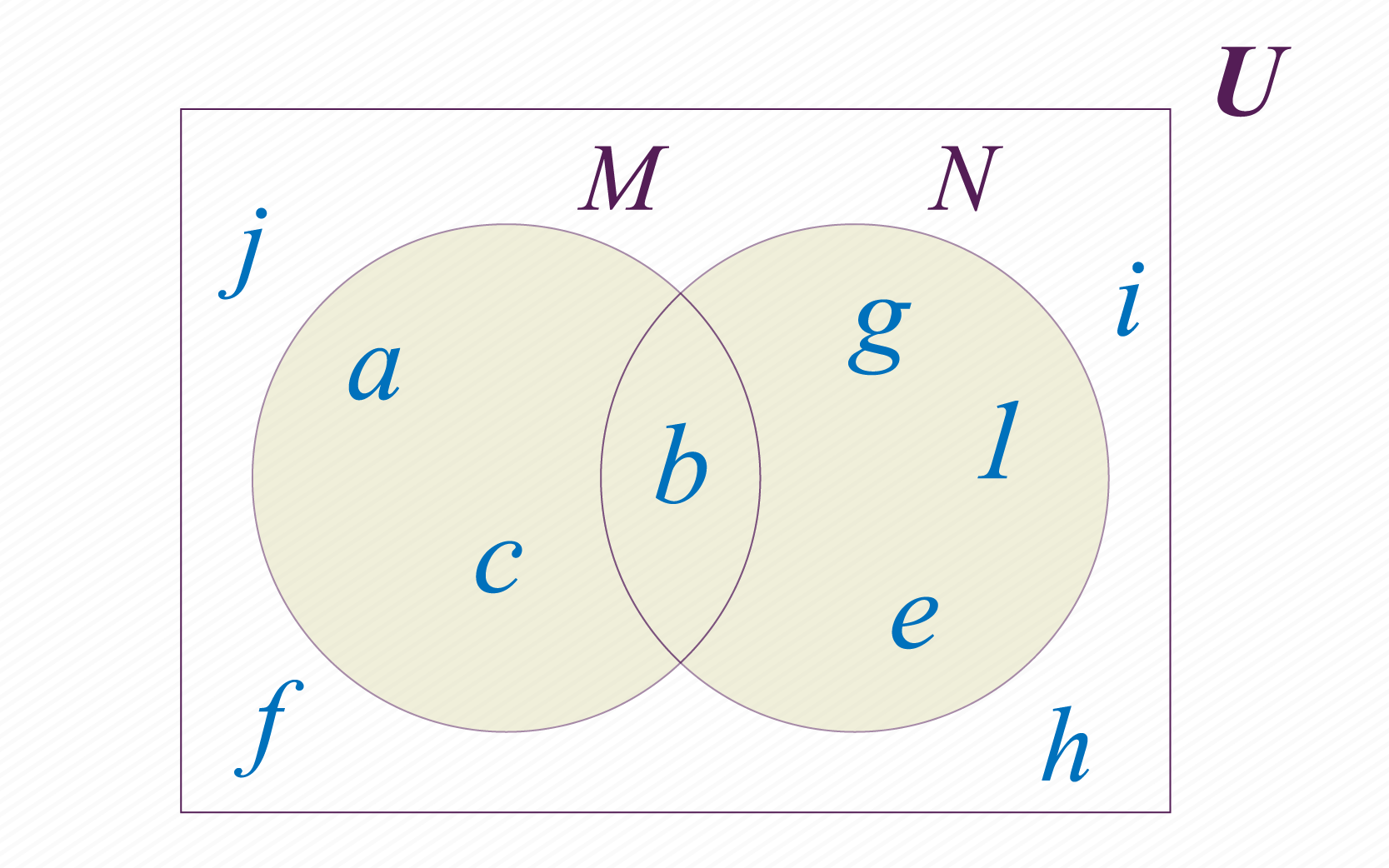
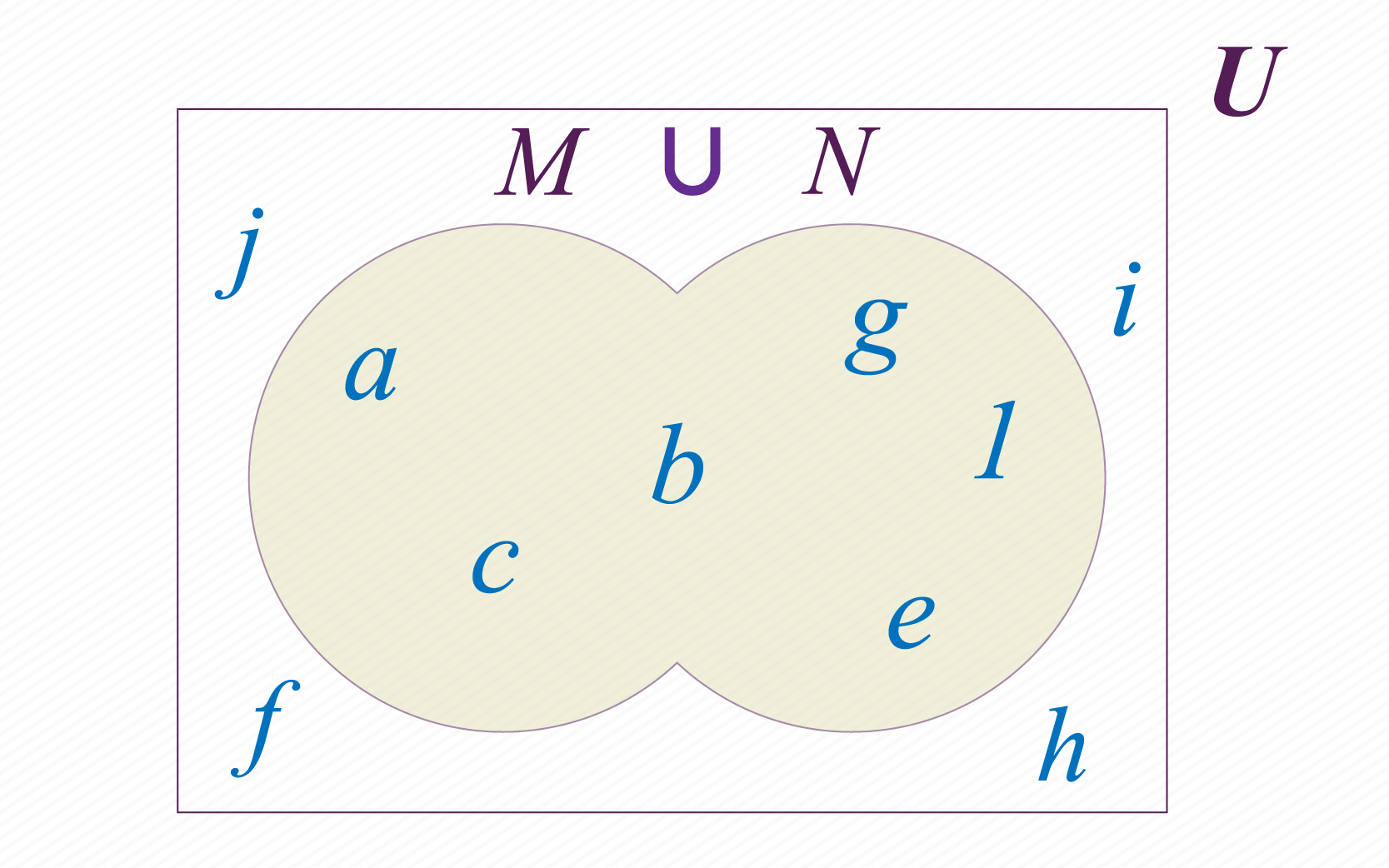
Podemos crear otro conjunto conformado con los elementos que pertenezcan a o a . A este nuevo conjunto le llamamos unión de y , y lo notamos de la siguiente manera: . En la imagen de abajo puedes observar el resultado de unir los conjuntos y .
Al elegir qué elementos estarán en la unión de nuestros conjuntos y , debes preguntarte cuáles están en el conjunto “o” en el conjunto . El resultado de la operación será el conjunto conformado por todos los elementos del conjunto universal , que cumplan la condición de estar en uno o en otro.
Tenemos en este caso: :
Intersección de conjuntos
Sigamos tomando como ejemplo los conjuntos y definidos anteriormente. Podemos determinar un nuevo conjunto conformado por los elementos que nuestros conjuntos y tienen en común. A este nuevo conjunto le llamamos intersección de y , y lo notamos de la siguiente manera: .
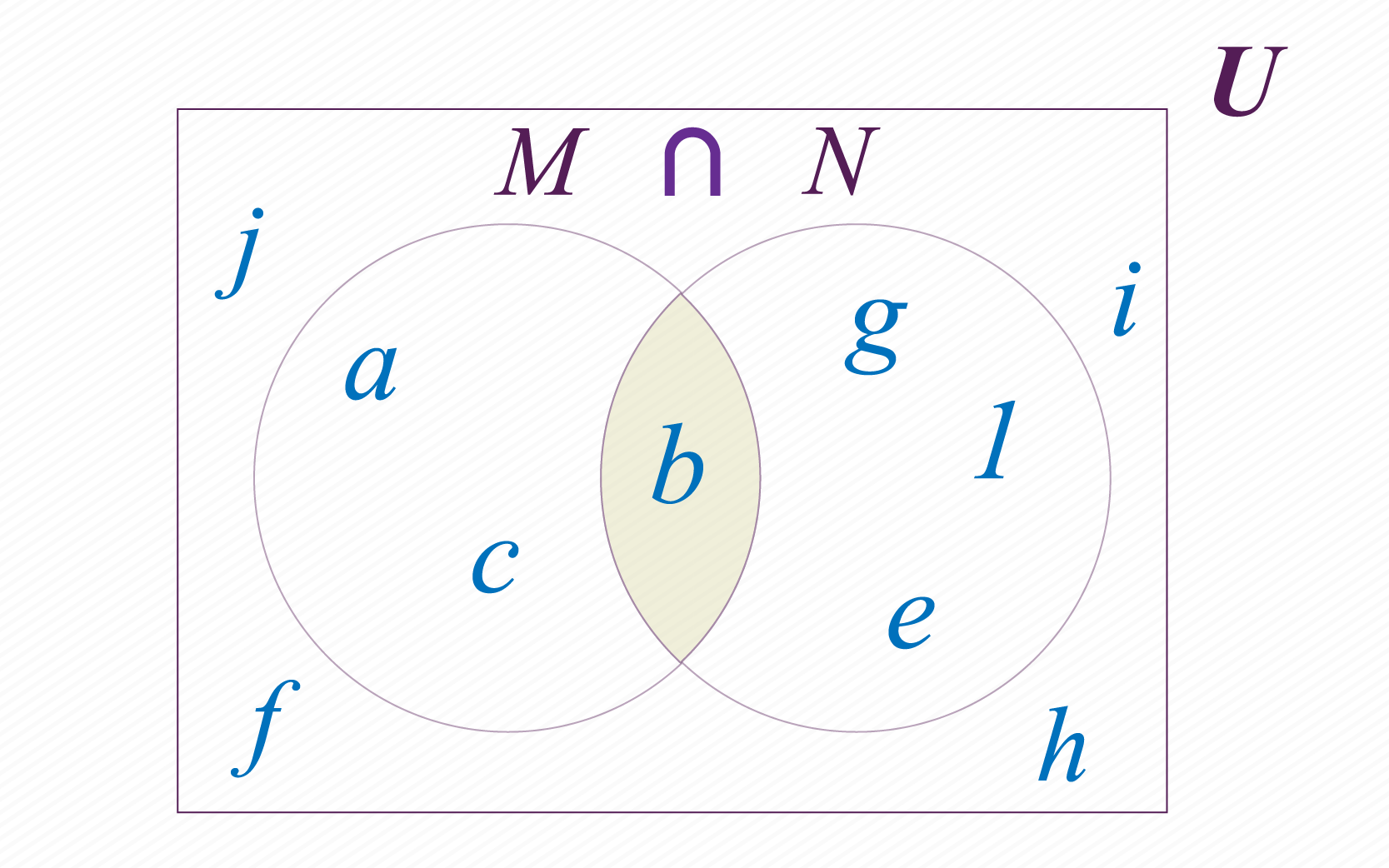
Para determinar que elementos pertenecen a la intersección de los conjuntos y te puedes preguntar qué elementos están en “y” en Todos los elementos del conjunto que cumplan esta condición deberán estar en el conjunto . En la figura de la arriba puedes ver la intersección de nuestros conjuntos y : .
Diferencia de conjuntos
En este caso se deben seleccionar los elementos de un conjunto que no estén en el otro. Por ejemplo, si realizas la operación menos , debes seleccionar los elementos de que no están en . Representamos la diferencia M menos N así: . Observa que en este caso .
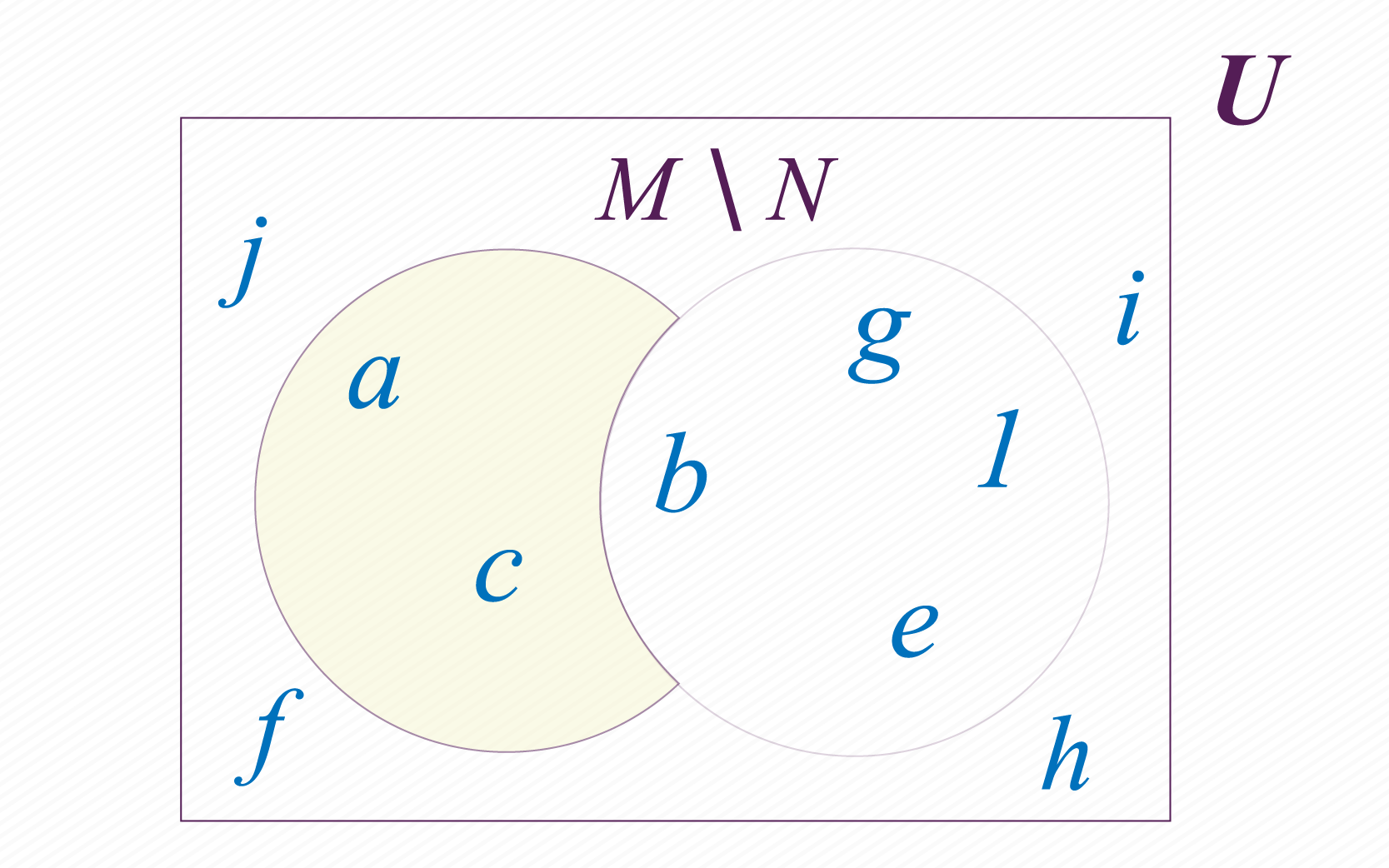
Diferencia simétrica de conjuntos
En esta ocasión se deben escoger los elementos de que no están en , y los elementos de que no están en . Puedes ver el resultado de la diferencia simétrica entre y en la figura de abajo. Representamos la diferencia simétrica a través del símbolo . En el caso de nuestros conjuntos y tenemos: .
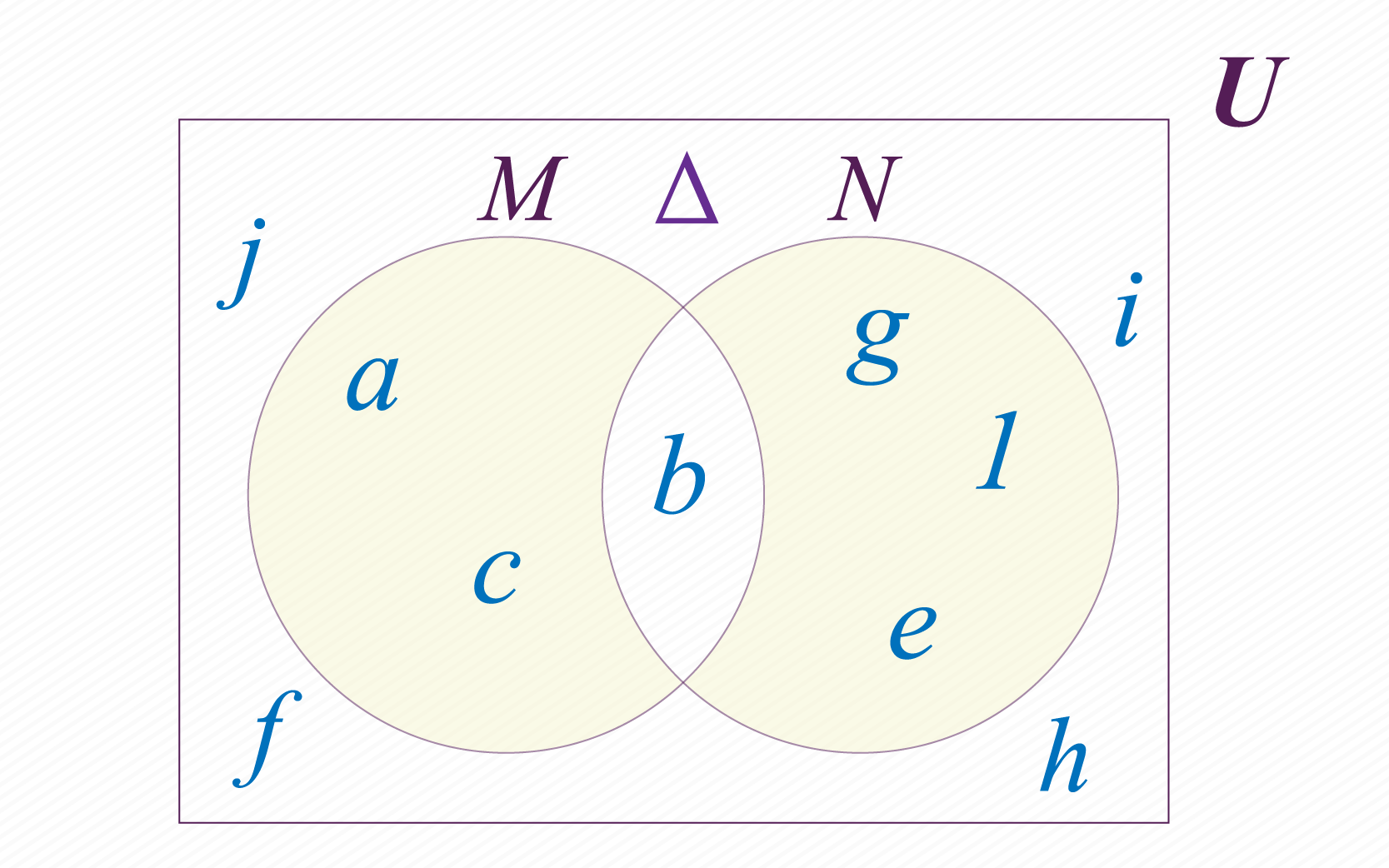
Complemento de un conjunto
La ultima operación que estudiaremos no es entre dos conjuntos. Decimos que el complemento de es el conjunto conformado por todos los elementos del conjunto universal , que no pertenecen al conjunto . Es común usar los símbolos , o para representar el complemento del conjunto . Nosotros usaremos el símbolo . En nuestro caso tenemos y .
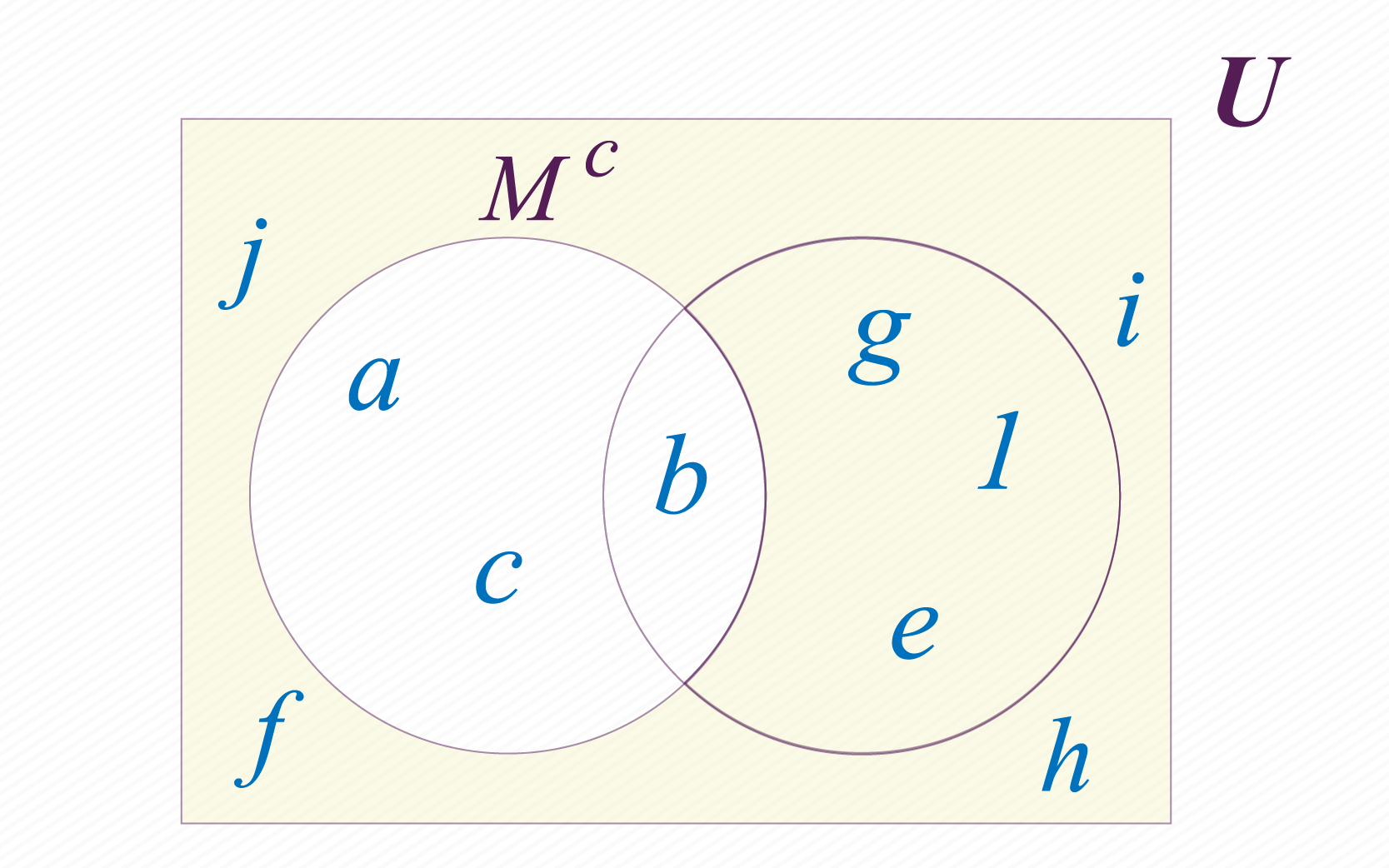
la suma y resta con números negativos
El mayor problema con los números negativos no son los números en si, sino las operaciones. Parece que hay tantas reglas que recordar.
Los números negativos son utilizados para representar diferentes situaciones en la vida cotidiana. Los encontramos por ejemplos:
- En la medida de la temperatura en un termómetro
- En la medida de la altitud terrestre (la elevación (montañas) versus la profundidad (en el mar))
- En las transacciones comerciales (ganar dinero versus tener deuda).
Cuando enseñas por primera vez las operaciones con números negativos, trata de conéctarlas con alguna situación concreta.
Yo tomaré por ejemplo la temperatura.
Suponiendo que n sea positivo, las reglas simples que hay que tomar en cuenta en esta situación son:
- x + n significa que la temperatura es x° y SUBE por n grados.
- x − n significa que la temperatura es x° y BAJA por n grados.
Se trata de MOVIMIENTO − mover n grados "arriba" o "abajo" en la escala del termómetro.
Por ejemplo:
- 6 − 7 significa: la temperatura es primero 6° y baja 7 grados.
- (-6) − 7 significa: la temperatura es primero -6° y baja 7 grados (¡se hace aun más frio!).
- (-2) + 5 significa: la temperatura es primero -2° y sube 5 grados.
- 4 + 5 significa: la temperatura es primero 4° y sube 5 grados.
Estas situaciones simples cubren cómo sumar un número positivo a cualquier entero, o cómo restar un número positivo de cualquier entero. Practíquelas en el principio, hasta que los niños se familiaricen con ellas.
Lo que nos queda es cómo sumar o restar un número NEGATIVO:
- (-2) + (-5) significaría: la temperatura es primero -2° y "añades" más negativos; entonces se hace más frio. La temperatura nueva es -7°.
El último caso es el menos intuitivo:
- 1 − (-5) o cómo restar un número negativo de otro entero. Personalmente, yo simplemente recuerdo la reglita de "dos signos negativos se convierten en un signo positivo".
Alguna gente lo explica así. En (-7) − (-3), puedes pensar que tienes 7 negativos primero, y "quitas" tres negativos, dejando cuatro negativos o -4
Esta regla de "dos negativos dan un positivo" puede parecer primero contraintuitiva, pero es necesaria para que varios principios de matemáticas continuen siendo validos (por ejemplo la propiedad distributiva).
La idea de "colecciones" funciona bien, para la ADICIÓN:
- 7 + (-4) significa que tienes una colección de 7 pelotas rojas y 4 pelotas azules. Una pelota roja y otra azul se "cancelan" o se hacen cero. El total será 3 pelotas rojas.
- (-3) + (-9) significa que tienes 3 pelotas azules y 9 pelotas azules más. El total es 12 pelotas azules, o -12.
Sin embargo, la idea de "movimiento" es una manera mucho más intuitiva para resolver problemas sencillos con los números enteros − excepto cuando estoy restando un número negativo, en cuyo caso convierto la resta en la suma de un número positivo.
Algunos libros presentan las reglas de sumar enteros en esta manera:
- Para sumar dos enteros con el mismo signo (ya sea positivo o negativo), suma sus valores absolutos y usa el mismo signo para el resultado.
- Para sumar dos enteros de signo distinto (uno positivo y el otro negativo), resta sus valores absolutos, y la respuesta (la suma) tendrá el mismo signo que el número con el valor absoluto mayor.
Luego esos libros expresan la resta como una suma (para luego poder aplicar las reglas de arriba), por ejemplo:
- 5 − 7 se convierte en 5 + (-7)
- (-4) − 2 se convierte en (-4) + (-2)
- y 5 − (-3) se convierte en 5 + 3.
Si bien son correctos, yo encuentro mucho más fácil usar la idea de "movimiento" para la mayor parte de las cuentas fáciles con enteros. Es más fácil comenzar de esa manera, y luego aprender las otras reglas para expresiones más complejas, tales como sumas con muchos sumandos o cuentas con decimales negativos.
Operaciones con fracciones
En esta página explicamos las operaciones entre fracciones (suma, resta, multiplicación y división) y resolvemos 10 problemas. Es necesario que sepáis calcular el mínimo común múltiplo y el máximo común divisor.
Índice:
- Conceptos necesarios
- Suma y resta de fracciones con denominador común
- Suma y resta de fracciones con distinto denominador
- Multiplicación de fracciones
- División de fracciones
- Fracción de un número
- Más problemas
1. Conceptos necesarios
Dada una fracción ,
es el numerador
es el denominador
Si dividimos un todo en partes iguales, la fracción son de estas partes:
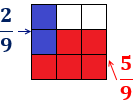
La fracción es irreductible si el máximo común divisor de y es 1. Esto significa que el resultado de la división es un número decimal.
Si una fracción no es irreductible, podemos transformarla en una fracción irreductible dividiendo el numerador y el denominador entre su máximo común divisor.
Otro método para simplificar es escribir numerador y denominador como productos para eliminar los factores comunes.
Más información y ejemplos de fracciones irreductibles en fracción irreductible.
La fracción es irreductible si el máximo común divisor de y es 1. Esto significa que el resultado de la división es un número decimal.
Si una fracción no es irreductible, podemos transformarla en una fracción irreductible dividiendo el numerador y el denominador entre su máximo común divisor.
Otro método para simplificar es escribir numerador y denominador como productos para eliminar los factores comunes.
Más información y ejemplos de fracciones irreductibles en fracción irreductible.
Números reales
¿Qué son los números reales?
Los números Reales, se denotan con la letra (R) y se definen como el conjunto de números que agrupa o incluye los números naturales (N), enteros (Z), racionales (Q) e irracionales (I).
También se puede decir, que cualquier número racional o irracional es un número real, R = Q ∪ I.
Por esta razón, se dice que todos los números pertenecen al conjunto R, excluyendo los números complejos. Tampoco son números reales:
- Las fracciones del tipo
 , ya que la división por cero no está definida. Por ejemplo
, ya que la división por cero no está definida. Por ejemplo  .
. - La raíz cuadrada de un número negativo
 , por no estar definida dentro de los números reales.
, por no estar definida dentro de los números reales.  .
. - La raíz par de cualquier número negativo de la formar
![\sqrt[n]{-b} \sqrt[n]{-b}](https://s0.wp.com/latex.php?latex=%5Csqrt%5Bn%5D%7B-b%7D&bg=f7f7f7&fg=000000&s=1) , donde "n"es un número par.
, donde "n"es un número par. ![\sqrt[4]{-16} \sqrt[4]{-16}](https://s0.wp.com/latex.php?latex=%5Csqrt%5B4%5D%7B-16%7D&bg=f7f7f7&fg=000000&s=1) .
.
El conjunto de los números reales tiene varias características, se dice con infinitos R ∈ (-∞,+∞). Siguen un orden y se pueden representar en la recta real. Por último, pueden ser expresados como un número decimal.
Por ejemplo, 4 se puede expresar como decimal 4,00. La fracción 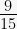 se expresa como el decimal 0,6. La raíz de un número;
se expresa como el decimal 0,6. La raíz de un número; 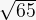 es igual a 8,062.
es igual a 8,062.
Los números Reales, se denotan con la letra (R) y se definen como el conjunto de números que agrupa o incluye los números naturales (N), enteros (Z), racionales (Q) e irracionales (I).
También se puede decir, que cualquier número racional o irracional es un número real, R = Q ∪ I.
Por esta razón, se dice que todos los números pertenecen al conjunto R, excluyendo los números complejos. Tampoco son números reales:
- Las fracciones del tipo
, ya que la división por cero no está definida. Por ejemplo
.
- La raíz cuadrada de un número negativo
, por no estar definida dentro de los números reales.
.
- La raíz par de cualquier número negativo de la formar
, donde "n"es un número par.
.
El conjunto de los números reales tiene varias características, se dice con infinitos R ∈ (-∞,+∞). Siguen un orden y se pueden representar en la recta real. Por último, pueden ser expresados como un número decimal.
Por ejemplo, 4 se puede expresar como decimal 4,00. La fracción se expresa como el decimal 0,6. La raíz de un número;
es igual a 8,062.
Propiedades de los números reales
El conjunto de los números reales (R), también satisface a diferentes propiedades de la matemática y se encuentran:
- Propiedad de cierre o cerradura: dice que la suma o multiplicación de dos números reales, siempre da como resultado un número real. Entonces para la suma, si a + b = c, c ∈ R. Ejemplo: 12 + 7 = 19, donde 19 pertenece a los números reales. Para la multiplicación, si a * b = c, c ∈ R. Ejemplo: 3 * 8 = 24, entonces 24 es también un número real.
- Propiedad conmutativa: el resultado de una suma o multiplicación es siempre igual, sin importar el orden en que se encuentren los números. Para la suma a + b = b + a, por tanto en la multiplicación a * b = b * a.
- Propiedad asociativa: la manera como se agrupen los números en una suma o multiplicación, no altera el resultado obtenido. Por tanto, en la suma (a + b) + c = a + (b + c) y para la multiplicación: (a * b) * c = a * (b * c).
- Propiedad distributiva: refiere que la multiplicación de un número por una suma o resta, es igual a la suma o diferencia de sus productos. Donde a(b ± c) = (a * b) ± (a * c).
- Propiedad modulativa o elemento neutro: en el caso de la suma, a cualquier número que se le sume 0, el resultado es igual al mismo número (a + 0 = a). En cambio, para la multiplicación cualquier número que se multiplique por 1, da como resultado el mismo número (a * 1 = a).
El conjunto de los números reales (R), también satisface a diferentes propiedades de la matemática y se encuentran:
- Propiedad de cierre o cerradura: dice que la suma o multiplicación de dos números reales, siempre da como resultado un número real. Entonces para la suma, si a + b = c, c ∈ R. Ejemplo: 12 + 7 = 19, donde 19 pertenece a los números reales. Para la multiplicación, si a * b = c, c ∈ R. Ejemplo: 3 * 8 = 24, entonces 24 es también un número real.
- Propiedad conmutativa: el resultado de una suma o multiplicación es siempre igual, sin importar el orden en que se encuentren los números. Para la suma a + b = b + a, por tanto en la multiplicación a * b = b * a.
- Propiedad asociativa: la manera como se agrupen los números en una suma o multiplicación, no altera el resultado obtenido. Por tanto, en la suma (a + b) + c = a + (b + c) y para la multiplicación: (a * b) * c = a * (b * c).
- Propiedad distributiva: refiere que la multiplicación de un número por una suma o resta, es igual a la suma o diferencia de sus productos. Donde a(b ± c) = (a * b) ± (a * c).
- Propiedad modulativa o elemento neutro: en el caso de la suma, a cualquier número que se le sume 0, el resultado es igual al mismo número (a + 0 = a). En cambio, para la multiplicación cualquier número que se multiplique por 1, da como resultado el mismo número (a * 1 = a).
Clasificación y tipos de números reales
Como se ha estudiado, el conjunto R, está formado por varios subconjuntos. En la imagen, se observa los 5 subconjuntos de números que pertenecen a los números reales.

- Números naturales: se indican con la letra N. Son los números no decimales mayores de 0. Pertenecen a este conjunto N = (1, 2, 3, 4, 5, 6, 7,…).
- Números enteros: el conjunto de los números enteros se identifica con la letra Z. Está formado por los números naturales y sus opuestos, es decir; por sus números negativos e incluye al 0. Donde Z = (-9, -8, -7, …, 0, 1, 2, 3, …). Estos números no tienen parte decimal ni fraccionaria.
Los números naturales están comprendidos dentro de los números en enteros. - Números racionales: son todos aquellos números que pueden ser escritos como una fracción de números enteros, donde el denominador debe ser diferente de 0. El conjunto de los racionales se denota con la letra Q =
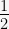 ,
,  ,
,  . El resultado de la fracción puede ser un número entero, decimal finito o semiperiódico.
. El resultado de la fracción puede ser un número entero, decimal finito o semiperiódico. - Números irracionales: su propio nombre lo indica, que no son racionales, por tanto, se definen como aquellos números que no pueden ser expresados como una fracción de números enteros. Son decimales que no se expresan ni de manera exacta ni periódica. Se identifican con la letra I = (
 , π, Φ,
, π, Φ, ![\sqrt[3]{19} \sqrt[3]{19}](https://s0.wp.com/latex.php?latex=%5Csqrt%5B3%5D%7B19%7D&bg=f7f7f7&fg=000000&s=1) …)
…)
Como se ha estudiado, el conjunto R, está formado por varios subconjuntos. En la imagen, se observa los 5 subconjuntos de números que pertenecen a los números reales.

- Números naturales: se indican con la letra N. Son los números no decimales mayores de 0. Pertenecen a este conjunto N = (1, 2, 3, 4, 5, 6, 7,…).
- Números enteros: el conjunto de los números enteros se identifica con la letra Z. Está formado por los números naturales y sus opuestos, es decir; por sus números negativos e incluye al 0. Donde Z = (-9, -8, -7, …, 0, 1, 2, 3, …). Estos números no tienen parte decimal ni fraccionaria.
Los números naturales están comprendidos dentro de los números en enteros. - Números racionales: son todos aquellos números que pueden ser escritos como una fracción de números enteros, donde el denominador debe ser diferente de 0. El conjunto de los racionales se denota con la letra Q =
,
,
. El resultado de la fracción puede ser un número entero, decimal finito o semiperiódico.
- Números irracionales: su propio nombre lo indica, que no son racionales, por tanto, se definen como aquellos números que no pueden ser expresados como una fracción de números enteros. Son decimales que no se expresan ni de manera exacta ni periódica. Se identifican con la letra I = (
, π, Φ,
…)
Ejemplos de números reales
Algunos ejemplos de números reales según su clasificación son:
Algunos ejemplos de números reales según su clasificación son:
Leyes de los exponentes
¿Qué son las leyes de los exponentes?
Las leyes de los exponentes son las que se aplican a aquel número que indica cuántas veces debe ser multiplicado por sí mismo un número base. Los exponentes también son conocidos como potencias. La potenciación es una operación matemática formada por una base (a), el exponente (m) y la potencia (b), que es el resultado de la operación.
Los exponentes son usados generalmente cuando son utilizadas cantidades muy grandes, debido a que estos no son más que abreviaciones que representan la multiplicación de ese mismo número una cantidad determinada de veces. Los exponentes pueden ser tanto positivos como negativos.
Las leyes de los exponentes son las que se aplican a aquel número que indica cuántas veces debe ser multiplicado por sí mismo un número base. Los exponentes también son conocidos como potencias. La potenciación es una operación matemática formada por una base (a), el exponente (m) y la potencia (b), que es el resultado de la operación.
Los exponentes son usados generalmente cuando son utilizadas cantidades muy grandes, debido a que estos no son más que abreviaciones que representan la multiplicación de ese mismo número una cantidad determinada de veces. Los exponentes pueden ser tanto positivos como negativos.
¿Qué son los exponentes en las operaciones matemáticas?
Como se dijo anteriormente, los exponentes son una forma abreviada que representa la multiplicación de números por sí mismos varias veces, donde el exponente solo se relaciona con el número de la izquierda. Por ejemplo:
23 = 2*2*2 = 8
En ese caso el número 2 es la base de la potencia, que será multiplicado 3 veces como lo indica el exponente, ubicado en la esquina superior derecha de la base. Existen diferentes formas de leer la expresión: 2 elevado a la 3 o también 2 elevado al cubo.
Los exponentes también indican el número de veces que pueden ser divididos, y para diferenciar esta operación de la multiplicación el exponente lleva el signo menos (-) delante de sí (es negativo), lo que significa que el exponente está en el denominador de una fracción. Por ejemplo:
2– 4 = 1/ 2*2*2*2 = 1/16
Esto no debe confundirse con el caso en el que la base es negativa, ya que dependerá de si el exponente es par o impar para determinar si la potencia será positiva o negativa. Así se tiene que:
– Si el exponente es par, la potencia será positiva. Por ejemplo:
(-7)2 = -7 * -7 = 49.
– Si el exponente es impar, la potencia será negativa. Por ejemplo:
(–2)5 = (-2)*(-2)*(-2)*(-2)*(-2)=-32.
Existe un caso especial en el cual si el exponente es igual a 0 se tiene que la potencia es igual a 1. También existe la posibilidad de que la base sea 0; en ese caso, dependiendo del exponente, la potencia será indeterminada o no.
Para realizar operaciones matemáticas con los exponentes es necesario seguir varias reglas o normas que hacen más simple hallar la solución de esas operaciones.
Como se dijo anteriormente, los exponentes son una forma abreviada que representa la multiplicación de números por sí mismos varias veces, donde el exponente solo se relaciona con el número de la izquierda. Por ejemplo:
23 = 2*2*2 = 8
En ese caso el número 2 es la base de la potencia, que será multiplicado 3 veces como lo indica el exponente, ubicado en la esquina superior derecha de la base. Existen diferentes formas de leer la expresión: 2 elevado a la 3 o también 2 elevado al cubo.
Los exponentes también indican el número de veces que pueden ser divididos, y para diferenciar esta operación de la multiplicación el exponente lleva el signo menos (-) delante de sí (es negativo), lo que significa que el exponente está en el denominador de una fracción. Por ejemplo:
2– 4 = 1/ 2*2*2*2 = 1/16
Esto no debe confundirse con el caso en el que la base es negativa, ya que dependerá de si el exponente es par o impar para determinar si la potencia será positiva o negativa. Así se tiene que:
– Si el exponente es par, la potencia será positiva. Por ejemplo:
(-7)2 = -7 * -7 = 49.
– Si el exponente es impar, la potencia será negativa. Por ejemplo:
(–2)5 = (-2)*(-2)*(-2)*(-2)*(-2)=-32.
Existe un caso especial en el cual si el exponente es igual a 0 se tiene que la potencia es igual a 1. También existe la posibilidad de que la base sea 0; en ese caso, dependiendo del exponente, la potencia será indeterminada o no.
Para realizar operaciones matemáticas con los exponentes es necesario seguir varias reglas o normas que hacen más simple hallar la solución de esas operaciones.
¿Cuáles son las leyes de los exponentes?
Primera ley: potencia de exponente igual a 1
Ejemplos
91 = 9.
221 = 22.
8951 = 895.
91 = 9.
221 = 22.
8951 = 895.
Segunda ley: potencia de exponente igual a 0
Ejemplos
10 = 1.
3230=1.
10950 = 1.
10 = 1.
3230=1.
10950 = 1.
Tercera ley: exponente negativo
Ejemplos
– 3-1 = 1/ 3.
– 6-2 = 1 / 62 = 1/36.
– 8-3 = 1/ 83 = 1/512.
– 3-1 = 1/ 3.
– 6-2 = 1 / 62 = 1/36.
– 8-3 = 1/ 83 = 1/512.
Cuarta ley: multiplicación de potencias con base igual
Para multiplicar potencias donde las bases son iguales y diferentes de 0, la base se mantiene y los exponentes son sumados: am * an = am+n.
Para multiplicar potencias donde las bases son iguales y diferentes de 0, la base se mantiene y los exponentes son sumados: am * an = am+n.
Ejemplos
– 44 * 43 = 44+3 = 47
– 81 * 84 = 81+4 = 85
– 22 * 29 = 22+9 = 211
– 44 * 43 = 44+3 = 47
– 81 * 84 = 81+4 = 85
– 22 * 29 = 22+9 = 211
Quinta ley: división de potencias con base igual
Para dividir potencias en las cuales las bases son iguales y diferentes de 0, se mantiene la base y los exponentes se restan como sigue: am / an = am-n.
Para dividir potencias en las cuales las bases son iguales y diferentes de 0, se mantiene la base y los exponentes se restan como sigue: am / an = am-n.
Ejemplos
– 92 / 91 = 9 (2 – 1) = 91.
– 615 / 610 = 6 (15 – 10) = 65.
– 4912 / 496 = 49 (12 – 6) = 496.
– 92 / 91 = 9 (2 – 1) = 91.
– 615 / 610 = 6 (15 – 10) = 65.
– 4912 / 496 = 49 (12 – 6) = 496.
Sexta ley: multiplicación de potencias con base diferente
Ejemplos
– 102 * 202 = (10 * 20)2 = 2002.
– 4511 * 911 = (45*9)11 = 40511.
Otra forma de representar esta ley es cuando una multiplicación se encuentra elevada a una potencia. Así, el exponente va a pertenecer a cada uno de los términos: (a*b)m=am* bm.
– 102 * 202 = (10 * 20)2 = 2002.
– 4511 * 911 = (45*9)11 = 40511.
Otra forma de representar esta ley es cuando una multiplicación se encuentra elevada a una potencia. Así, el exponente va a pertenecer a cada uno de los términos: (a*b)m=am* bm.
Ejemplos
– (5*8)4 = 54 * 84 = 404.
– (23 * 7)6 = 236 * 76 = 1616.
– (5*8)4 = 54 * 84 = 404.
– (23 * 7)6 = 236 * 76 = 1616.
Séptima ley: división de potencias con base diferente
Ejemplos
– 303 / 23 = (30/2)3 = 153.
– 4404 / 804 = (440/80)4 = 5,54.
De igual forma, cuando una división se encuentra elevada a una potencia, el exponente va a pertenecer en cada uno de los términos: (a / b) m = am /bm.
– 303 / 23 = (30/2)3 = 153.
– 4404 / 804 = (440/80)4 = 5,54.
De igual forma, cuando una división se encuentra elevada a una potencia, el exponente va a pertenecer en cada uno de los términos: (a / b) m = am /bm.
Ejemplos
– (8/4)8 = 88 / 48 = 28.
– (25/5)2 = 252 / 52 = 52.
Existe el caso en que el exponente es negativo. Entonces, para que sea positivo el valor del numerador se invierte con el del denominador, de la siguiente manera:
– (a / b)-n = (b / a )n = bn / an.
– (4/5) -9 = ( 5 / 4) 9 = 59 / 44.
– (8/4)8 = 88 / 48 = 28.
– (25/5)2 = 252 / 52 = 52.
Existe el caso en que el exponente es negativo. Entonces, para que sea positivo el valor del numerador se invierte con el del denominador, de la siguiente manera:
– (a / b)-n = (b / a )n = bn / an.
– (4/5) -9 = ( 5 / 4) 9 = 59 / 44.
Octava ley: potencia de una potencia
Cuando se tiene una potencia que esta elevada a otra potencia —es decir, dos exponentes a la vez—, la base se mantiene y los exponentes se multiplican: (am)n=am*n.
Cuando se tiene una potencia que esta elevada a otra potencia —es decir, dos exponentes a la vez—, la base se mantiene y los exponentes se multiplican: (am)n=am*n.

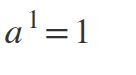
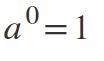
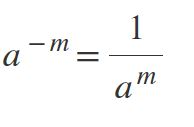
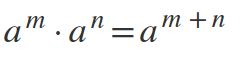
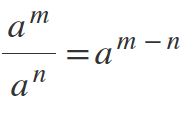
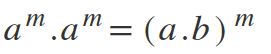
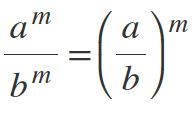
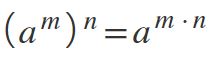
Comentarios
Publicar un comentario